簡單回顧
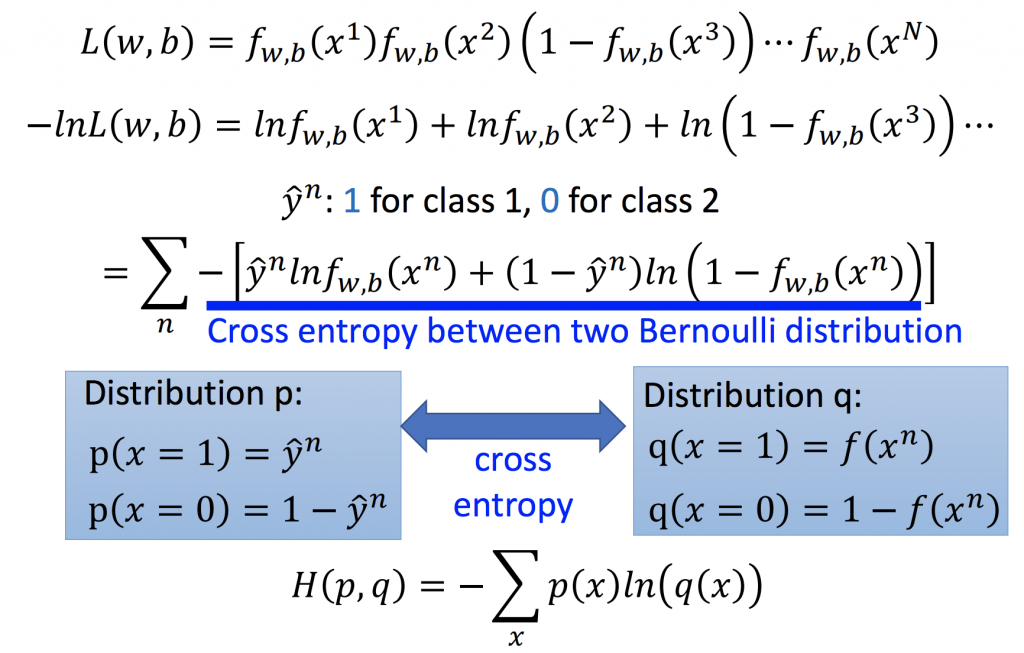
前幾章提到的linear classificaton、linear regression及logistic regression，其實都有共通的地方，都必須透過特徵值及權重做計算，由下圖便可以清楚地看到:

• linear classificaton: 計算出來的值必須判斷是正或負來做分類，err就是判斷分隊或分錯來做修正
• linear regression: 計算出來的值就直接輸出，err是square err
• logistic regression: 算出來的值必須再通過sigmoid function做輸出（因為我們想要的是0~1的值）
  

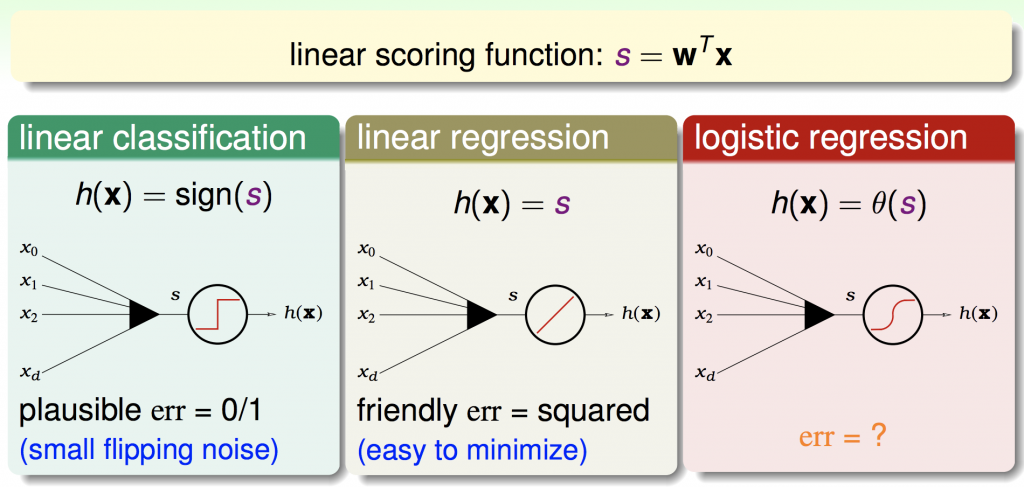
資料產生的機率
假設training data是由某個probabilaty所產生的，也就是給定一組w, b產生N筆training data（如下圖所示）。x1屬於C1，所以它被產生的機率為fw,b(x1)，x2屬於C2，所以它被產生的機率為fw,b(x2)，x3屬於C2，但我們要算的是屬於C1的機率，所以它被產生的機率為(1-fw,b(x3))…
那所要找的w, b就是要找能夠最大化我們training data的w, b（有點饒口），這邊要求的就是Maximum Likelihood，可以參考我的ML_Day3(classification)，這邊有更詳細介紹。

簡化 Maximum Likelihoodru及 cross-entropy
因為Maximum Likelihood是一個連乘的符號，為了方便計算式子，把它變成連加的符號，就像linear regression在計算error時取最小值，所以會對式子取 ln（如下圖所示）。

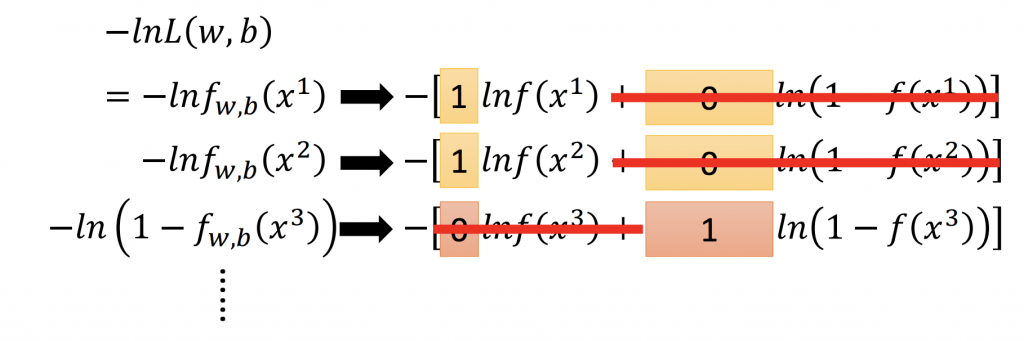
經過整理之後可以得到，cross-entropy的式子，它所代表的含義就是p, q這兩個distribution有多接近，就會把它定義成是loss function。假如這兩個distribution一模一樣，那計算出來的cross-entropy就是0。